知乎原帖复现
  • 这里产生的幂律分布方法是：
1
2
3
4
5
x_min = 1
alpha = 3.5
# 产生一组均匀分布的随机数
rnd_list = np.random.uniform(0, 1, 10**5)
x_list = x_min * np.power(1 - rnd_list, -1 / (alpha - 1))
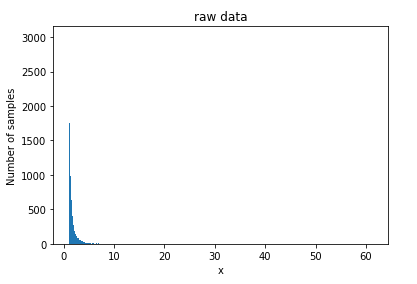
原始数据直方图

image-20201025083106759

log-log图

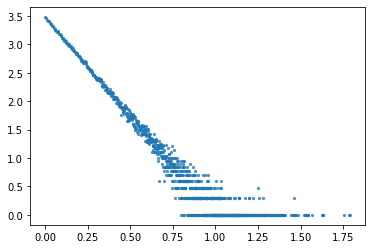
image-20201025083134937

log-log图
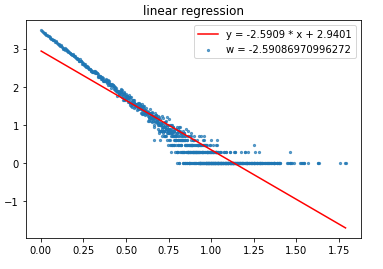
经过线性回归的log-log图

image-20201025083236920

$$ \alpha = 2.59 \tag{1} $$

经过指数/对数分箱之后，进行了参数估计

这里在分箱之前没有处理，所以最后得到的alpha = -w + 1的

从原贴看出，作者在最后进行参数估计的时候，将分箱的数量大大减少。

image-20201025083330912

$$ \alpha = 3.50 \tag{2} $$

转化到0-1
思路

由原帖，推知的幂律分布公式：$ x = x_{min}(1-r)^{-1\over -(\alpha-1)} $，因为要得到$ x \in (0, 1)$, 所以就是要求函数r的定义域，但是发现比较难求，转换为求原始函数$ r = 1-({x\over x_{min}})^{-(\alpha-1)}$的在$ x \in (0, 1)$的值域。

发现在$ r < 0$时，$ x \in (0, 1)$。

这里有一个问题就是 ：对这个负值的取值问题

负值的取值，与随机出来的幂律分布的下限存在一定关系。负值取得越小越接近零，但是其上限可能也会随之减小。

大样本的尝试
1
2
3
4
5
6
7
参数
r (-5000, 0)---------------------幂律分布的最大最小值0.03314199326291829 0.9516629536071909
bin = 5000
rnd_list = np.random.uniform(-5000, 0, 10**5)
0.03314199326291829 0.9516629536071909
# 对数指数分箱
intervals = np.logspace(-2, 0, 100, base = 10)
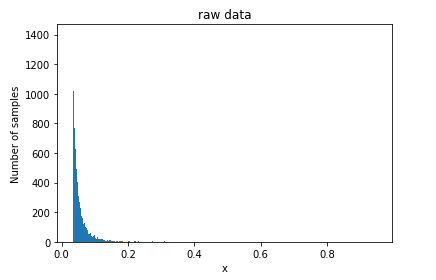
原始数据

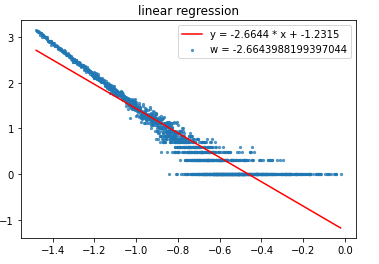
均匀分箱：log-log图以及线性回归

image-20201025101310804

大样本均匀分箱：$$ \alpha = 2.66 \tag{3} $$

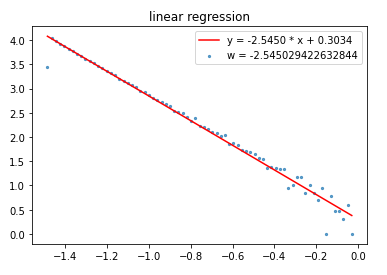
指数/对数分箱：参数估计

image-20201025101401753

大样本指数/对数分箱：$$ \alpha = 3.54 \tag{4} $$

小样本尝试
1
2
3
4
5
参数
bin = 500
rnd_list = np.random.uniform(-5000, 0, 2000)
0.033144970720553266 0.6949274551386315
intervals = np.logspace(-1.5, 0, 15, base = 10)
原始数据

image-20201025101901111

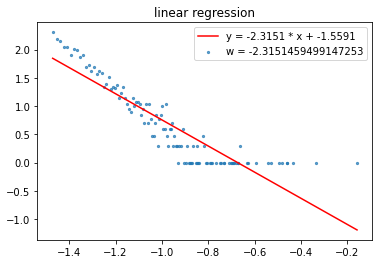
均匀分箱：log-log图以及线性回归

image-20201025101936791

小样本均匀分箱：$$ \alpha = 2.31 \tag{5} $$

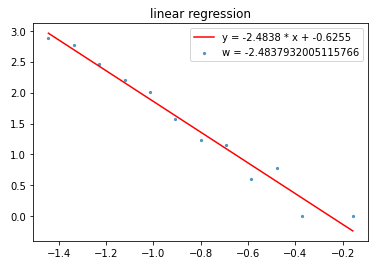
指数/对数分箱：参数估计

image-20201025101957870

小样本指数/对数分箱：$$ \alpha = 3.48 \tag{6} $$

源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
import numpy as np
import math
import random
from sklearn import linear_model
import matplotlib.pyplot as plt

x_min = 1
alpha = 3.5
# 产生一组均匀分布的随机数
rnd_list = np.random.uniform(0, 1, 10**5)
print(rnd_list)
x_list = x_min * np.power(1 - rnd_list, -1 / (alpha - 1))
print(x_list)
hist_h, hist_x = np.histogram(x_list, bins=5000)
print(len(hist_h))
print()
# 对于刚得到的数据进行可视化
plt.title('raw data')
plt.xlabel('x')
plt.ylabel('Number of samples')
plt.hist(x_list, bins=5000)
plt.show()
# 画一个log-log图

y = hist_h
x = []
# 对于hist_x得到的5001个分箱的边缘，那么，是不是取中间会更好
pre = 0
for current in range(1, len(hist_x)):
    xt = (hist_x[pre] + hist_x[current]) / 2
    x.append(xt)
    pre = current
print(len(x))
start = 0.5
log_x = np.log10(x)
log_y = np.log10(y)
plt.scatter(log_x[0:5000], log_y, s=5, alpha=0.7)
plt.show()
################################################################################
# 之后要进行方法化，以便后续调用
################################################################################
# 进行线性回归
# 线性回归的数据准备
reg_x = []
reg_y = []
for i, j in zip(log_x, log_y):
    # 这里手动把一些log(0)给过滤掉，否则无法正常进行线性回归的训练
    if (not np.isinf(i)) and (not np.isinf(j)):
        reg_x.append([float(i)])
        reg_y.append(float(j))
# 实例化一个线性函数
regr = linear_model.LinearRegression()
regr.fit(reg_x, reg_y)
w = regr.coef_
b = regr.intercept_
item = 'y = %.4f * x + %.4f' %(w[0], b)
print(item)
# 画出线性回归拟合得到的直线
plt.title('linear regression')
plt.scatter(log_x[0:5000], log_y, s=5, alpha=0.7)
plt.plot(reg_x, regr.predict(reg_x), color='red')
plt.legend(labels=[item, 'w = '+ str(w[0])], loc='upper right')
plt.show()


# Exponential binning 进行指数/对数分箱，这里我发现在原有的5000次分箱的时候结果依旧不好，但是我看作者在这里把分箱的个数做的也比较少，所以我这里也仅取了100个分箱
intervals = np.logspace(0,np.log10(100000+10),100,base = 10)
print(len(intervals))

hist_h1, hist_x1 = np.histogram(x_list, bins=intervals)
y1 = hist_h1
x1 = []
# 对于hist_x得到的5001个分箱的边缘，那么，是不是取中间会更好
pre = 0
for current in range(1, len(intervals)):
    xt = (intervals[pre] + intervals[current]) / 2
    x1.append(xt)
    pre = current
print(len(x))
start = 0.5
log_x1 = np.log10(x1)
log_y1 = np.log10(y1)
plt.scatter(log_x1, log_y1, s=5, alpha=0.7)
plt.show()



# 加上线性回归
reg_x1 = []
reg_y1 = []
for i, j in zip(log_x1, log_y1):
    # 这里手动把一些log(0)给过滤掉，否则无法正常进行线性回归的训练
    if (not np.isinf(i)) and (not np.isinf(j)):
        reg_x1.append([float(i)])
        reg_y1.append(float(j))
# 实例化一个线性函数
regr1 = linear_model.LinearRegression()
regr1.fit(reg_x1, reg_y1)
w = regr1.coef_
b = regr1.intercept_
item = 'y = %.4f * x + %.4f' %(w[0], b)
print(item)
# 画出线性回归拟合得到的直线
plt.title('linear regression')
plt.scatter(log_x1[0:5000], log_y1, s=5, alpha=0.7)
plt.plot(reg_x1, regr1.predict(reg_x1), color='red')
plt.legend(labels=[item, 'w = '+ str(w[0])], loc='upper right')
plt.show()