复杂网络研究关心的问题

  • 如何构建一个复杂网络。反问题
  • 如何刻画一个复杂网络，如何描述一个复杂网络的结构及其性质.例如我们统计网络的度的分布
  • 关注网络是如何发展为当前这种结构的，也就是网络是如何演化的
  • 网络演化到特定结构的后果。比如，这种结构是否具有鲁棒性， 网络上动力学行为如何刻画等。正问题：在已知网络结构的情况下，去分析网络的性质

复杂网络分析的统计量

概念讲解

度 、平均度、 度分布、路径、介数、集聚系数、邻接矩阵、距离与网络直径

介数：针对节点的统计量，是指通过节点的最短路径的条数

距离与网络直径：两个节点之间最短路径称为距离。一个网络中的最大距离称为网络的直径。

集聚系数：是衡量网络是否紧密聚集，即网络内部是否有很多成团现象的指标。一个节点的聚集系数是这个节点的所有的邻居节点中，实际相连的节点对占全部可能相连的节点对的比值。网络的集聚系数是每个节点系数的平均值。

image-20201121194054152

随机图：ER Model

随机图模型是一个基本的网络模型，属于baseline，经常与其他的图结构进行性质上的比较。特点很多，比如：节点多，当节点的平均度很小的时候度分布符合泊松分布。

随机网络有两种机制模型，他们描述了两种不同但是性质相似的两种随即网络的建立过程。

  • C(N, p): N个节点，任何两个节点以p概率连接
  • C(N, L): N个节点，L条边，每个节点连接边的概率是相等的

奇异点: 度极大或者是极小的点。

随机图中就没有奇异点，因为随机图中每个点连接边的概率是相等的。

小世界网络

六度分隔理论：世界上的任何两个人，只需5、6个人就能相互认识。大概意思就是我们世界从这个角度来看其实很小。

小世界网络模型构建：

  • 两个不同节点之间至多一条边
  • 不能与自身相连
  • $p$ 是重连概率

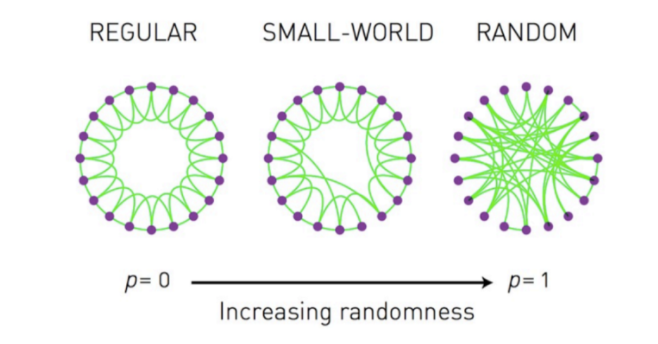
image-20201121200244740

小世界网络就是，相对于同等规模节点的随机网络：

  • 具有较短平均路径长度
  • 较大的聚类系数

产生这种特征的原因是，存在捷径的添加。捷径就是，在随机重连的过程中添加的长边。

具有小世界特征的动力系统中的，信息的传播能力、计算能力等都得到了增强。

文献阅读

无标度网络

无标度网络：是指那些度分布符合幂律分布的网络。有两大特征：

  • 具有自相似结构 (网络局部与整体在结构特性上是相似的，网络不具有明显的尺度特征—无标度)
  • 两极分化，高度弥散 (幂律分布)

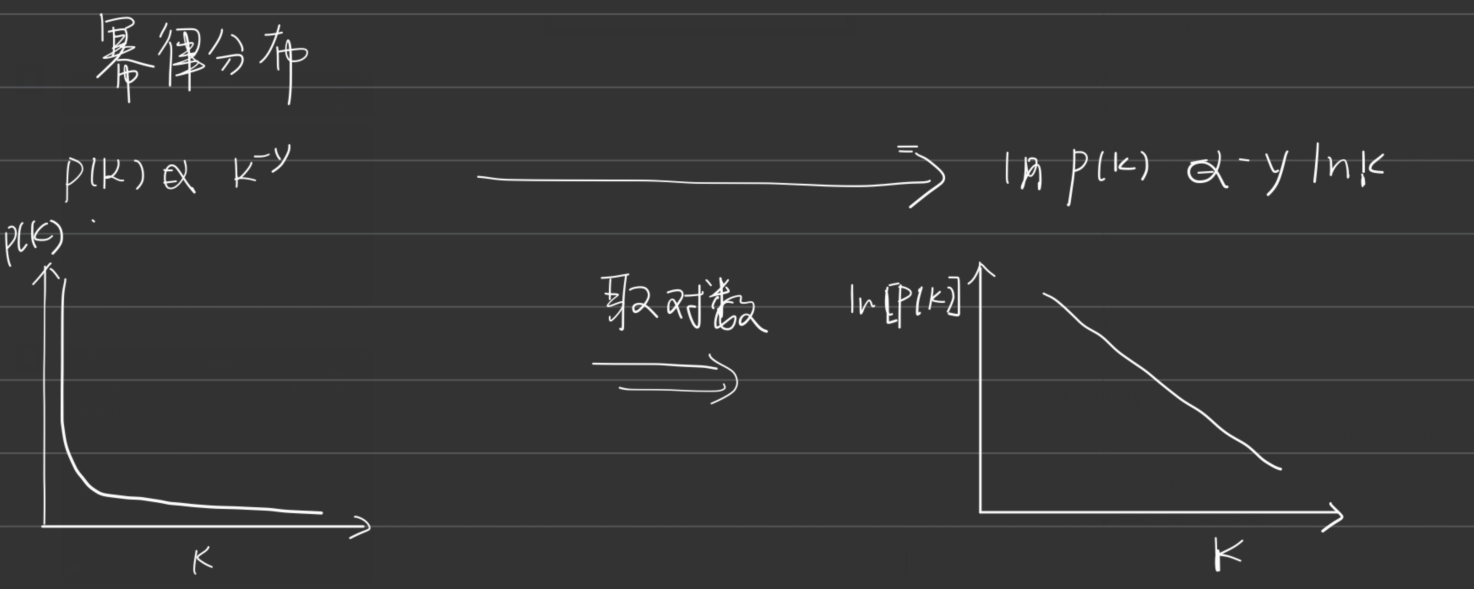
image-20201121202903145

无标度网络的演化：

BA模型

节点数量不断增大，网络规模不断扩大。产生的新节点更愿意去连接那些连接数比较大的节点，遵循偏好连接的机制。在BA模型中，增长与偏好连接非常重要。

文献阅读

网络中的度相关

网络中平均度是对网络的粗略描述，度分布可以让我们对网络的了解更加的具体，但是也不能完全的刻画网络的结构特性。有些时候，有相同度分布的网络可能展现出不同的性质和行为，所以引入匹配性(度相关)。

度分布就是我们选取图中的一个节点，度为k的概率。但是度相关是我们选取一条边的两个节点，节点度为j和k的联合概率，所以我们可以将度相关看为2阶度分布。

度的相关与无关

如果我们拿出的一条边的两个节点度值是完全随机的，则我们认为这两个节点的度值是无关的，则成为这个网络不具有相关性，否则这个网络就是相关的。

如果大度的节点更倾向于连接大度节点，则我们称这个网络是正相关(同配)的，否则称这个网络是负相关(异配)的。为了刻画这种相关的程度，我们还可以发明，同配系数作为量化指标。

加权网络

网络连边上的权重衡量的节点之间的相互作用的强度。为了更好的理解和衡量网络的性质。

  • 如何对网络加权

  • 权重如何帮我们更好的理解网络的性质

1.权重的加入为我们提供了审视网络的全新视角，例如，我们可以衡量网络的权重分布

2.权重的加入也可以让我们更精确的衡量原有统计指标的意义

文献阅读

复杂网络中的社团结构

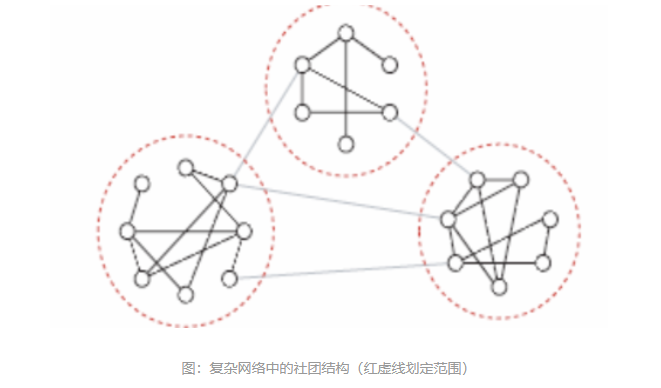
image-20201121213520901

我们可以通过宏观或者是微观的一些量来研究一个复杂网络。社团结构是介于微观与宏观之间，是我们对于复杂网络的一种中观视角。

描述性的角度来定义:

社团结构，它指的是复杂网络中的一个局部，这个局部内部的链接很稠密，但这个局部与其他社团的链接则很稀疏。

如何找到网络中的社团结构

评价方法–Q函数

Q函数的输出是一个标量，越接近于1说明划分的结果越好。

划分方法

  • 基于网络拓扑结构的方法，比如：层次聚类法
  • 基于网络上的动力学方法，这种方法的核心思路是在网络上定义某种动力学，让网络进行演化，对时间演化数据序列进行分析，从而得到社团结构。
  • 基于Q函数的优化方法，转化为优化问题。

网络上节点的重要性

首先，我们需要一个度量指标，即测度，来合理的度量节点的重要性–中心性。

度中心性、介数中心性、接近度中心性

网络上的动力学

网络上的动力学, 就是网络上的节点如何相互影响的一种描述。

1
例如，在传染病动力学中，所有的节点都有健康，染病，恢复这三种状态，如果在某时刻，一个节点的大部分邻居都处于染病状态，那么下一时刻这一节点很可能遭受感染——其自身的状态将会由健康变为染病。

参考